概率分布与熵编码
在端到端图像/视频压缩模型中,我们需要去尽可能精准地模拟待编码元素值的概率分布。一方面是为了更精确地进行码率估计,另一方面也是因为更精准的概率分布建模能使得熵编码环节更好地消除统计冗余节省码字。
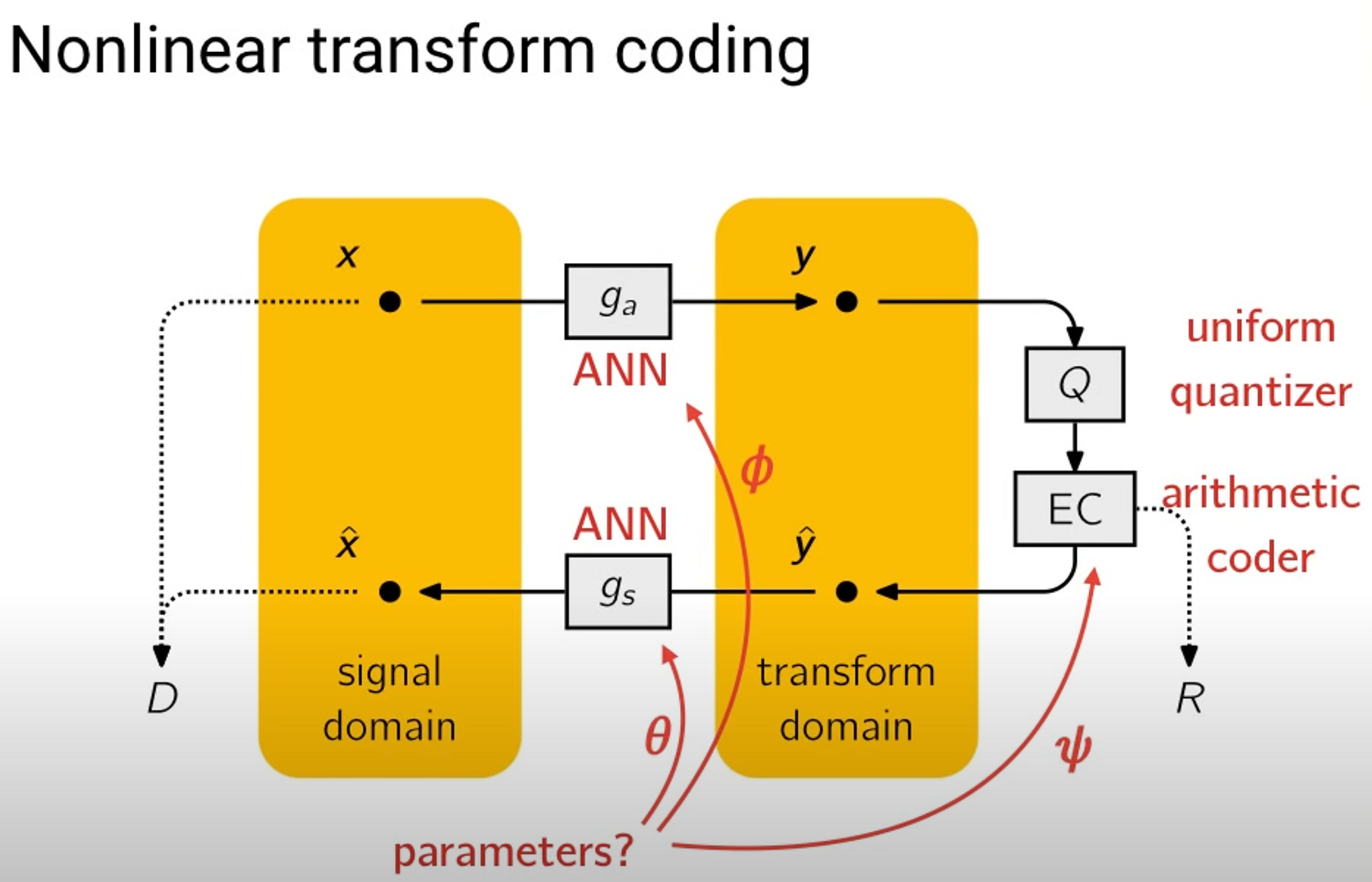
建模出概率分布后,在实际熵编码中,就可以通过概率分布生成熵编码器所需要的概率表。
多说一句,在传统编解码里,通常熵编码会采用自适应模型,即随着编码字符的输入,不断更新概率分布(自适应模型相比静态模型效率更高,符合局部性原理,适应符号概率忽大忽小的波动,如果能合理地利用上下文信息压缩效率可以远超静态模型)。然而在端到端压缩模型里,通常直接通过网络生成独立的概率分布的参数,不会随着编码过程更新概率表。
量化不可导
这个没什么好说的,量化四舍五入的取整操作显然是不可导的,所以在训练的时候可以通过加均匀噪声来替换四舍五入的操作。
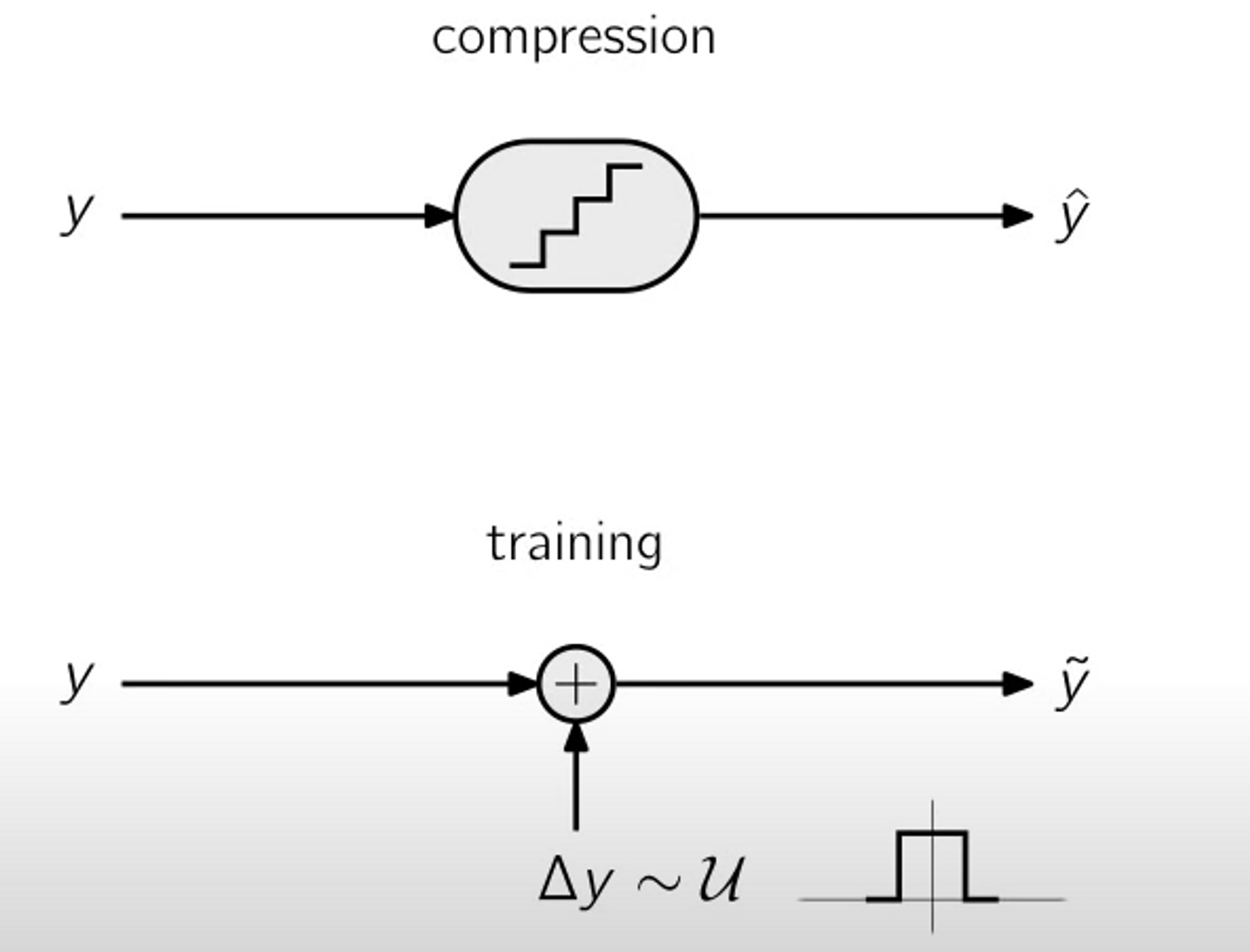
在训练阶段,我们会通过给待编码元素值加上-0.5到0.5的均匀噪声来替代量化操作。而实际推理的时候,就正常进行量化。
均匀噪声涉及到的概率关系
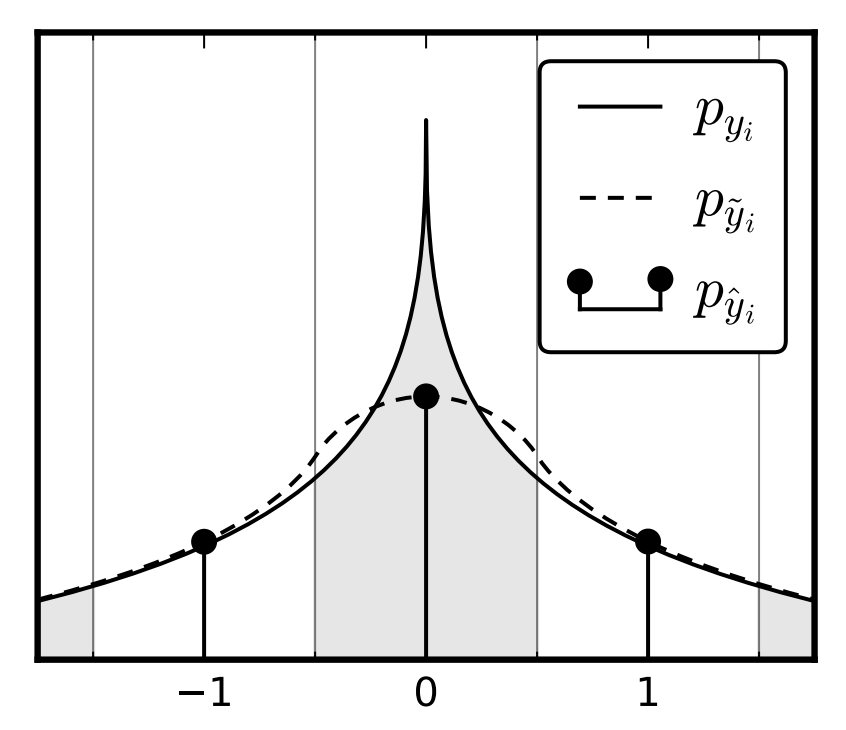
首先明确一下这几条线分布代表什么。
$p_{y_i}$:编码空间元素值的概率密度函数
$p_{\tilde{y_i}}$:$y_i$ 加上均匀噪声后的概率密度函数
$p_{\hat{y_i}}$:$y_i$量化后的概率质量函数(量化后就成了离散型变量了)
均匀噪声其实就是均匀分布 $U(-0.5, 0.5)$,$y_i$ 加上均匀噪声得到 $\tilde{y_i}$,两个独立的连续随机变量的和的概率分布公式是 $f_{X+Y}(z) = \int_{-\infty}^{\infty} f_X(x) f_Y(z-x) ,\mathrm{d}x$,直观来说也很好理解,对于任意 $\tilde{y_i}$ 值为 $c$,可能加均匀噪声得到 $c$ 的 $y_i$ 取值范围其实就是 $c-0.5$ 到 $c+0.5$,$p_{\tilde{y_i}}$ 在 $c$ 点的值其实就可以通过 $p_{y_i}$ 在 $c-0.5$ 到 $c+0.5$ 的积分得出。
对于每个整数点,也自然符合上述描述。
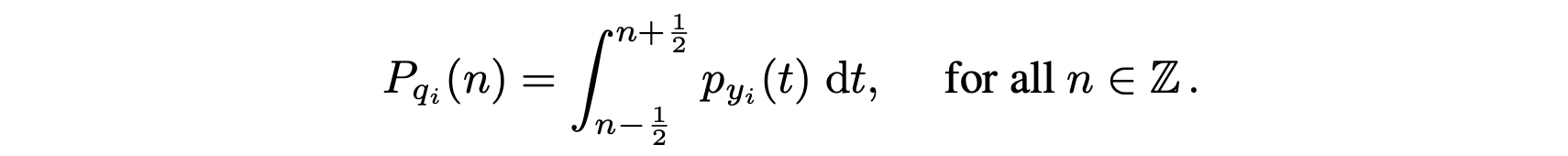
而这样一来,加均匀噪声得到的 $p_{\tilde{y_i}}$ 最妙的性质就在于,在每个整数点 $p_{\tilde{y_i}}$ 的值和实际量化得到的离散变量 $p_{\hat{y_i}}$ 在这一点的概率质量相等。
所以说,加均匀噪声这一操作,本质上类似于在给 $p_{\hat{y_i}}$ 的概率质量函数作插值,类似于一个连续松弛 (continuous relaxation) 的操作。
此外,我们在端到端模型里通常去建模的也就是这个 $p_{y_i}$,而这里其实是假设 $p_{y_i}$ 近似一个拉普拉斯分布,实际代码实现中,有一部分模型采用拉普拉斯分布去建模,也有一部分模型,比如 CompressAI,是采用高斯分布去建模的。
CompressAI 代码中的熵模型
以其中的 GaussianConditional 熵模型为例,稍微讲一下实际实现的时候一些常见操作。
def forward(
self,
inputs: Tensor,
scales: Tensor,
means: Optional[Tensor] = None,
training: Optional[bool] = None,
) -> Tuple[Tensor, Tensor]:
if training is None:
training = self.training
outputs = self.quantize(inputs, "noise" if training else "dequantize", means)
likelihood = self._likelihood(outputs, scales, means)
if self.use_likelihood_bound:
likelihood = self.likelihood_lower_bound(likelihood)
return outputs, likelihood
训练的时候和上面说的一样,通过加均匀噪声替代量化操作。
而其中这个 likelihood 其实就是用于码率估计的,网络会输出 $y_i$ 值,然后我们叠加均匀噪声,而网络也会输出 $p_{y_i}$ 建模为高斯分布的 $\mu$ 和 $\sigma$ 值,这样其实我们就能计算出当前条件下 $p_{\tilde{y_i}}$ 的特定取值。后面再用 $-log_2 x$ 就能算出估计出的码字比特大小。
再来看一下实际熵编解码的实现,以编码为例。
def compress(self, inputs, indexes, means=None):
"""
Compress input tensors to char strings.
Args:
inputs (torch.Tensor): input tensors
indexes (torch.IntTensor): tensors CDF indexes
means (torch.Tensor, optional): optional tensor means
"""
symbols = self.quantize(inputs, "symbols", means)
if len(inputs.size()) < 2:
raise ValueError(
"Invalid `inputs` size. Expected a tensor with at least 2 dimensions."
)
if inputs.size() != indexes.size():
raise ValueError("`inputs` and `indexes` should have the same size.")
self._check_cdf_size()
self._check_cdf_length()
self._check_offsets_size()
strings = []
for i in range(symbols.size(0)):
rv = self.entropy_coder.encode_with_indexes(
symbols[i].reshape(-1).int().tolist(),
indexes[i].reshape(-1).int().tolist(),
self._quantized_cdf.tolist(),
self._cdf_length.reshape(-1).int().tolist(),
self._offset.reshape(-1).int().tolist(),
)
strings.append(rv)
return strings
symbols 就是量化后的待编码值减去网络预测出的高斯分布的均值,这样后面熵编码就可以统一用准备好的不同方差的零均值高斯采样的 cdf 表。再注意一下这里的 indexes ,下文会讲。
上面说的 cdf 表可以通过这个更新函数看一下实现过程。
def update(self):
multiplier = -self._standardized_quantile(self.tail_mass / 2)
pmf_center = torch.ceil(self.scale_table * multiplier).int()
pmf_length = 2 * pmf_center + 1
max_length = torch.max(pmf_length).item()
device = pmf_center.device
samples = torch.abs(
torch.arange(max_length, device=device).int() - pmf_center[:, None]
)
samples_scale = self.scale_table.unsqueeze(1)
samples = samples.float()
samples_scale = samples_scale.float()
upper = self._standardized_cumulative((0.5 - samples) / samples_scale)
lower = self._standardized_cumulative((-0.5 - samples) / samples_scale)
pmf = upper - lower
tail_mass = 2 * lower[:, :1]
quantized_cdf = torch.Tensor(len(pmf_length), max_length + 2)
quantized_cdf = self._pmf_to_cdf(pmf, tail_mass, pmf_length, max_length)
self._quantized_cdf = quantized_cdf
self._offset = -pmf_center
self._cdf_length = pmf_length + 2
可以看到,cdf 表其实是一定数量采样的 scale 值对应的零均值高斯分布(转化后的 $p_{y_i}$)在一定数量采样点上计算好 $p_{\tilde{y_i}}$ 的值。
这里其实有两处采样:
- 采样 scale (对应 index ,index 指明取 cdf 表哪个分布)
- 对于分布采样一系列的点计算概率值 (对应 cdf 表中每个分布)
可以通过 build_indexes 来看一下 indexes 的确定过程。
def build_indexes(self, scales: Tensor) -> Tensor:
scales = self.lower_bound_scale(scales)
indexes = scales.new_full(scales.size(), len(self.scale_table) - 1).int()
for s in self.scale_table[:-1]:
indexes -= (scales <= s).int()
return indexes
indexes 是通过 scales 来确定的,具体来说 index 其实是之前说的一系列采样的 scale 值里小于等于当前 scale 的最接近它的采样 scale 的编号。
最后修改于 2022-04-20