传统熵模型
算术编码 (Arithmetic Coding)
流程
(以静态模型举例)
- 假设有一段数据需要编码,统计里面所有的字符和出现的次数。编码从初始区间 (0, 1] 开始。
- 在当前区间内根据各字符概率划分子区间。
- 读入字符,找到该字符落入的子区间,将区间更新为该子区间,并重复 2, 3 步骤
- 最后得到的区间 [low, high) 中任意一个小数以二进制形式输出即得到编码的数据
例子如下:
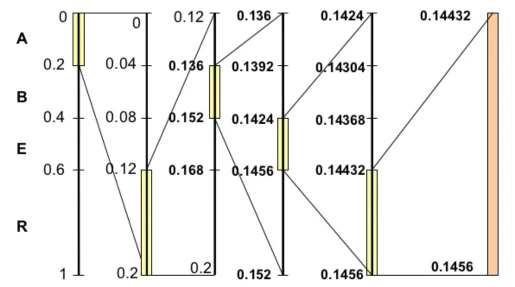
实现细节
最后结果是一个小数,我们不能简单地用一个 double 类型去表示和计算这个小数,因为根据数据的复杂程度,这个小数可能任意长,小数点后可能会有成千上万位。
然而,小数点后的数据前几位很有可能是在过程中是可以不断提前确定的。例如如果当前区间为 [0.14432, 0.1456),高位的 0.14 可以提前确定,14已经可以输出了。那么小数点可以向后移动两位,区间变成 [0.432, 0.56),在此基础上进行后面的计算。这样编码区间永远保持在一个有限的精度要求上。
上述是基于十进制的,实际数字是用二进制表示的,当然原理是一样的,用十进制只是为了表述方便。
静态模型 → 自适应模型
静态模型在初始时对完整的数据统计完概率分布,之后不再更新概率分布;自适应模型随着字符的输入会不断更新概率分布。
静态模型的缺点在于:
- 在压缩前对信息内字符进行统计的过程会消耗大量时间。
- 对较长的信息,静态模型统计出的符号概率是该符号在整个信息中的出现概率,而自适应模型可以统计出某个符号在某一局部的出现概率或某个符号相对于某一上下文的出现概率,换句话说,自适应模型得到的概率分布将有利于对信息的压缩(可以说结合上下文的自适应模型的信息熵建立在更高的概率层次上,其总熵值更小),好的基于上下文的自适应模型得到的压缩结果将远远超过静态模型。
例如一段码流,某符号在前面出现概率较大而后面概率小,甚至忽大忽小,采用自适应模型就可以更好的适应这样的变动,压缩效率会比静态模型更高。主流视频编码标准如H.264/H.265都使用自适应模型。
算术编码 vs 哈夫曼编码
首先说结论,算术编码压缩效率更高,哈夫曼编码复杂度更低。
这两种编码,或者说熵编码的本质是,概率越小的字符,用更多的 bit 去表示,这反映到概率区间上就是,概率小的字符所对应的区间也小,因此这个区间的上下边际值的差值越小,为了唯一确定当前这个区间,则需要更多的数字去表示它。
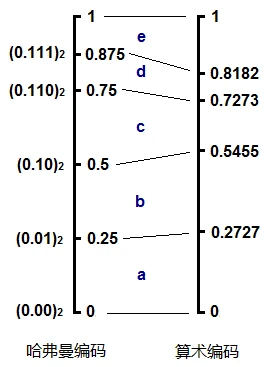
哈夫曼编码由于不断地二叉,它的子区间总是 $\frac{1}{2}$ 的幂次方。而算术编码可以做到严格按照概率的大小等比例划分子区间。所以哈夫曼编码只是算术编码一种粗略的近似。
CABAC
CABAC(Context-based Adaptive Binary Arithmetic Coding),CABAC 被视频标准H.264/H.265所采用。
CABAC可以分为二值化、上下文建模和二进制算术编码三个步骤。
其中上下文建模相当于把整段码流进行了再次的细分,把相同条件下的字符bin(比如块大小/亮度色度/语法元素/扫描方式/周围情况等)归属于某个context,形成一个比较独立的子队列而进行编码,其更新只与当前的状态和当前字符是否MPS有关(换句话说,只和历史该子队列编码字符和当前字符有关),而与别的子队列/字符是无关的。当然输出码字往往是根据规则而“混”在一起的。
CABAC虽然性能很好,但也存在以下几点不足:
- 复杂度过高,不易并行处理。存在块级依赖(左/上角的块没有码率估计/熵编码,后继块就无法得到更新后的状态,从而无法开始码率估计/熵编码)、Bin级依赖(同一个子队列的bin存在前后依赖性,后继的bin要等前面bin编完后才能得到更新后的上下文状态)以及编码的几个环节依赖,这些依赖性会影响编码器的并行实现。
- 计算精度问题。为简化计算,CABAC采用128个状态来近似,根据原来状态和当前符号性质查表得到下个状态。这个过程中会有一些精度的损失。另外,如果当一连串的MPS到来,状态到达62后就不会继续改变,只会“原地踏步”。换句话说,当概率到达0.01975时就不会随着符号继续变小,这样会影响压缩效率。
- Context的设计问题。部分context利用频率很低,在测试中平均一帧都用不到几次,而有的context使用频率很高,需要进一步的优化。
区间编码 (Range Coding)
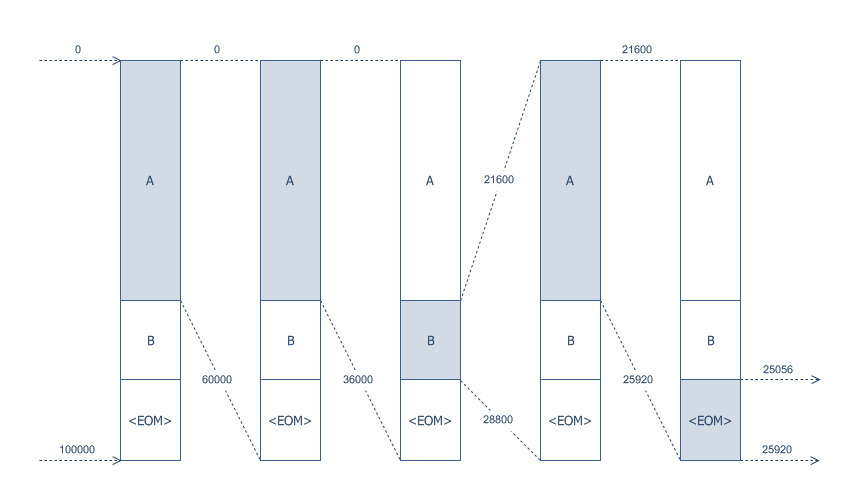
区间编码可以看为算术编码的一个变种,比算术编码压缩效率略小,但运算速度近乎是算术编码的两倍。
区间编码在整数(任意底)空间中进行进行计算,而算术编码的区间总是以小数的形式进行迭代。其他部分都几乎一样。
端到端熵模型
Todo…
参考
最后修改于 2021-12-05