如何评价重建图像的质量:比较重建图像与原始图像的可视误差。
MSE
Mean Squared Error, 均方误差
$MSE = \frac{1}{N}\sum\limits_{i=1}^{N}(x_i-y_i)^2$
两者越接近,MSE 越小。MSE 损失的范围为 0 到 ∞。
PSNR
Peak Signal to Noise Ratio,峰值信噪比,即峰值信号的能量与噪声的平均能量之比,通常取 log 单位为分贝。
$PSNR = 10 log_{10}\frac{MaxValue^2}{MSE}$
从式子可以看出 PSNR 可以理解为 MSE 的另一种表达形式。与 MSE 相反的是,重建图像质量越好,PSNR 数值越大。
对于图像来说,像素点数值以量化方式保存,八比特位深的情况,取值范围为 [0, 255],$MaxValue$ 就是 255。
SSIM
MSE 与 PSNR 的问题是,在计算每个位置上的像素差异时,其结果仅与当前位置的两个像素值有关,与其它任何位置上的像素无关。这种计算差异的方式仅仅将图像看成了一个个孤立的像素点,而忽略了图像内容所包含的一些视觉特征,特别是图像的局部结构信息。而图像质量的好坏极大程度上是一个主观感受,其中结构信息对人主观感受的影响非常之大。
而 SSIM (Structural Similarity,结构相似性) 就试图解决这个问题
SSIM 由三部分组成:
- 亮度对比 平均灰度作为亮度测量: $\mu_x = \frac{1}{N}\sum\limits_{i=1}^{N}x_i$ 亮度对比函数: $l(x,y) = \frac{2\mu_x\mu_y + C_1}{\mu_x^2+\mu_y^2+C_1}$
- 对比度对比 灰度标准差作为对比度测量: $\sigma_x={(\frac{1}{N-1}\sum\limits_{i=1}^N{(x_i-\mu_x)}^2)}^{\frac{1}{2}}$ 亮度对比函数: $c(x,y)=\frac{2\sigma_x\sigma_y+C_2}{\sigma_x^2+\sigma_y^2+C_2}$
- 结构对比 结构测量: $\frac{x-\mu_x}{\sigma_x}$ 结构对比函数: $s(x,y) = \frac{\sigma_{xy}+C_3}{\sigma_x\sigma_y + C_3}$
SSIM 函数:
$SSIM(x,y)={[l(x,y)]}^\alpha \cdot {[c(x,y)]}^\beta \cdot {[s(x,y)]}^\gamma$
$一般取 \alpha = \beta =\gamma=1$
$SSIM(x,y)=\frac{(2\mu_x\mu_y+C_1)(2\sigma_x\sigma_y+C_2)}{(\mu_x^2+\mu_y^2+C_1)(\sigma_x^2\sigma_y^2+C_2)}$
下图是同样 MSE 的图片,仅仅做对比拉伸(灰度拉伸,增大图像灰度级的动态范围)、均值偏移,其实不怎么影响人眼对图像的理解,而模糊和压缩痕迹则影响较大,这些情况下 SSIM 就能更好地做出判断。

MS-SSIM
SSIM 算法基于 HVS 擅长从图像中提取结构信息,并利用结构相似度计算图像的感知质量。但 SSIM 是一种单尺度算法,实际上正确的图像尺度取决于用户的观看条件,如显示设备分辨率、用户的观看距离等。
单尺度的 SSIM 算法可能仅适用于某个特定的配置,为了解决该问题,MS-SSIM (Multi-scale structural similarity) 在 SSIM 算法的基础上提出了多尺度的结构相似性评估算法。
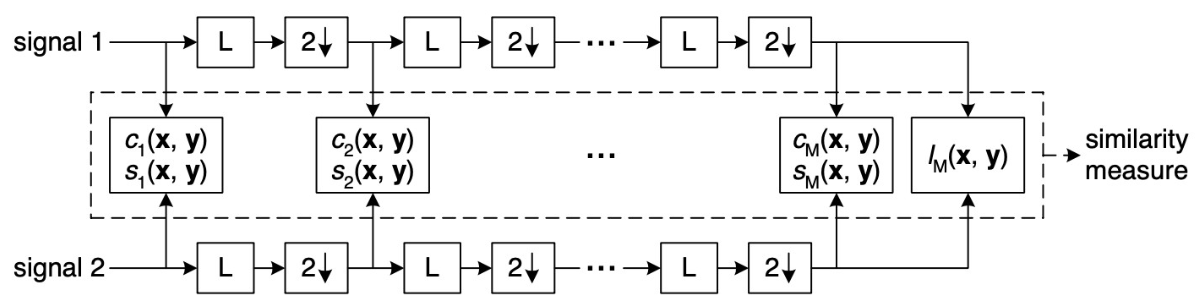
MS-SSIM 算法,L 表示低通滤波器,2↓ 表示采样间隔为 2 的下采样
原始图像的尺度为 1,最大尺度为 M,对 $scale=j$ 的尺度而言,其亮度、对比度、结构的相似性分布表示为 $l_j(x,y), c_j(x,y), s_j(x,y)$,MS-SSIM 的计算公式为:
$MS-SSIM(x,y) = {[l_M(x,y)]}^{\alpha M} \cdot \prod\limits_{j=1}^M{[c_j(x,y)]}^{\beta j}{[s_j(x,y)]}^{\gamma j}$
一般,令 $\alpha_j = \beta_j = \gamma_j$,$j \in [1, M]$,我们得到:
$MS-SSIM(x,y) = {[l_M(x,y)]}^{\alpha M} \cdot \prod\limits_{j=1}^M{[c_j(x,y) \cdot s_j(x,y)]}^{\alpha j}$
最后修改于 2021-12-02