引子

生成模型

能从可学习的概率分布中采样得到样本的模型。

在一些生成模型中，样本通过将随机的隐层变量送入网络生成得到。

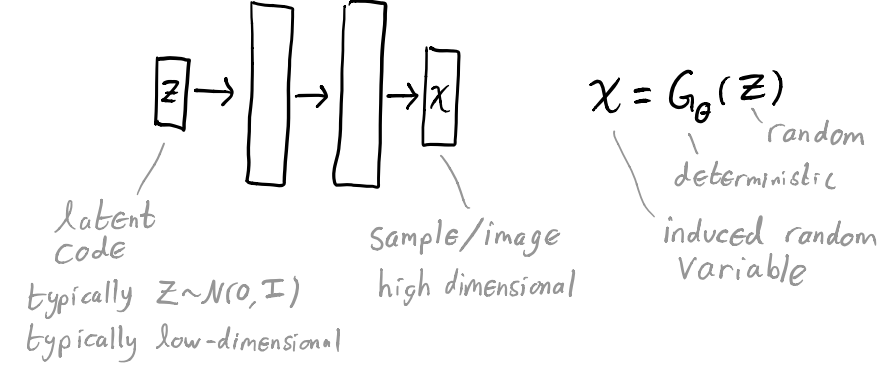
自编码器 AE

自编码器通过学习从输入到隐层和从隐层到输出的映射来重建信号/图像。

目标：$X’ = D_\theta(E_\phi(X)) \approx X$

$\mathop{min}\limits_{\theta, \phi} \sum\limits_{i=1}^n||D_\theta(E_\phi(X_i))-X_i||^2$，其中 ${{X_i}}_{i=1\cdots n}$ 为数据集。

自编码器并不是一种生成模型，因为它并没有定义一个概率分布，无法采样。

自编码器 → 生成模型？

我们会有一个很自然的做生成模型的想法，那就是训练一个从低维隐层变量生成观测样本的生成模型，最大化观测数据似然。

假设这个生成模型为 $G_{\theta}:\mathbb{R}^k \rightarrow \mathbb{R}^d$，其中 $k < d$，将隐层变量 $Z$ 映射为样本 $X$，那么其实在样本空间里几乎大部分区域 $p(X)=0$。

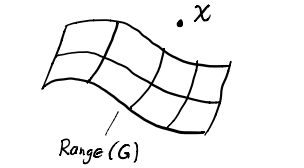
如果我们从样本空间看，在这个高维空间只会有非常小的一个低维空间子集 $p(X)$ 是有值的，并且我们在训练的时候其实是不知道这个子集的分布的，而其余大部分区域 $p(X)=0$，也就意味着我们很难直接优化似然。

但是有一种方法可以让我们在每一处都得到非零值，那就是在已有先验 $p(Z)$ 的条件下，定义一个有噪声的观测模型 $p_\theta(X|Z)=\mathcal{N}(X;G_\theta(Z), \eta I)$ (其中 $\eta$ 是可调整的参数，$I$ 是单位矩阵)。

所以 $p(X) = \int p(Z)p(X|Z)\mathrm{d}Z$，这个值也很难去计算，所以我们不是去优化 $p(X)$ 而是去优化 $p(X)$ 的下限（变分推断里的证据下限 ELBO，后面会证明）。

那么这其实就是 VAE 的雏形了。

变分自编码器 VAE

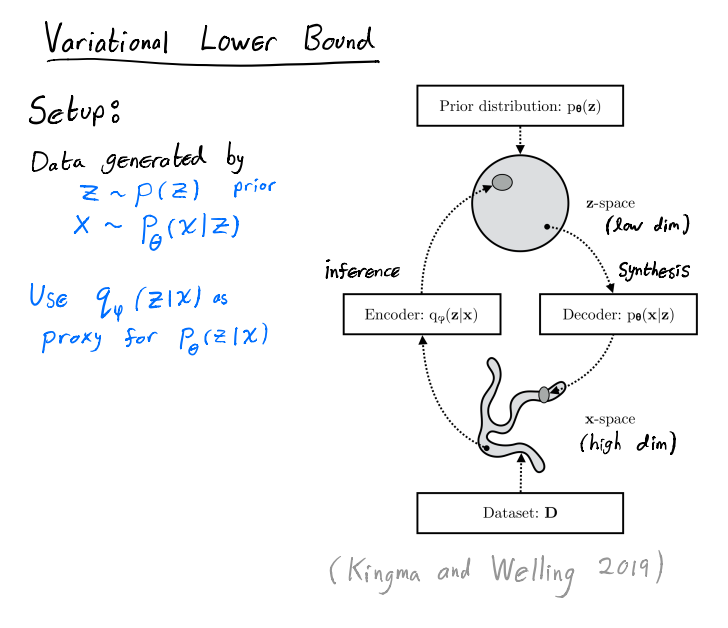
上面的图是 VAE 的整体思路，生成的部分也是也就是 decoder 的部分，我们会假设 $Z$ 服从一个简单的先验分布 $p(Z)$，这个分布可以是一个标准正态分布。通过 decoder 会得到高维图像空间的一个概率分布。

而 encoder 端，注意 VAE 有一个很重要的想法是，我们不去直接计算难以计算的 $p_\theta(Z|X)$，而是用另外单独学习的网络去模拟一个 $q_\phi(Z|X)$，它其实是 $p_\theta(Z|X)$ 的一个近似。

$p_\theta(X)$ 推导

再看一下 $p_\theta(X)$ 下界的推导过程。①：因为 $p_\theta(X)$ 是独立于 $Z$ 的，所以我们可以去计算它在 $Z$ 上的期望；②：条件概率公式；③：上下约一个 $q_\phi(Z|X)$；④：右边的项其实就是 $q_\phi(Z|X)$ 和 $p_\theta(Z|X)$ 的 KL 散度，KL 散度衡量的是两个概率分布之间的相似性，两者差异越小，KL 散度越小，两分布完全一致时 KL 散度才为 0，所以因为右项恒大于等于 0，我们可以把左项视为 $log\space p_\theta(X)$ 的下界。之后就不直接优化 $log\space p_\theta(X)$，而是优化这个下界。

Variational Lower Bound 的直观解释

再来看一下怎么理解这个变分下界，注意我们的目标是最大化这个下界。首先用条件概率公式替换一下，之后把式子拆成两部分，下面来解释一下为什么第一项是重建误差，第二项是正则项。

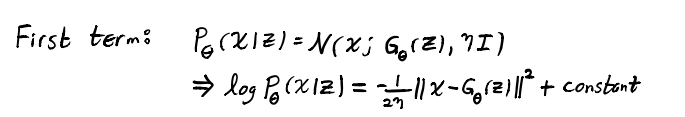
之前说了我们建立了一个有噪声的观测模型 $p_\theta(X|Z)=\mathcal{N}(X;G_\theta(Z), \eta I)$ (就是 $Z$ 通过 decoder 后得到的那个高维图像空间的分布)，正态分布的公式不用说了吧，代入一下就会发现第一项是一个 L2 距离，最大化这个负的 L2 距离就是在减小重建误差，encourage $q_\phi$ to be point mass，这句话我是这么理解的，point mass 其实是离散的概率分布，减小重建误差就是在消除我们加的这个高斯噪声，让它成为类似于我们最先讲的那个被舍弃的点到点的离散概率模型（但注意它又是连续概率，所以就是接近奇异分布？）。

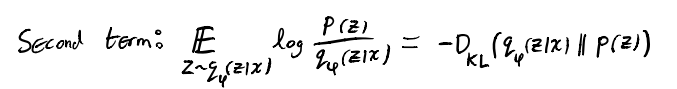
再看第二项，这一项可以写成一个 KL 散度，我们最大化负的这个 KL 散度就是在让 $q_\phi(Z|X)$ 和 $p(Z)$ 两个概率分布尽可能接近。上一项重建损失是鼓励 $q_\phi$ 去成为 point mass，这里则是平滑 $q_\phi$ 去使它尽可能接近标准正态分布。

可以看到两项之间存在相驳的张力，前一项试图让 $q_\phi$ 成为奇异分布，后一项则试图让 $q_\phi$ 不要成为奇异分布。可以理解为前者鼓励它准，后者鼓励它具有更强的生成性。

VAE 架构

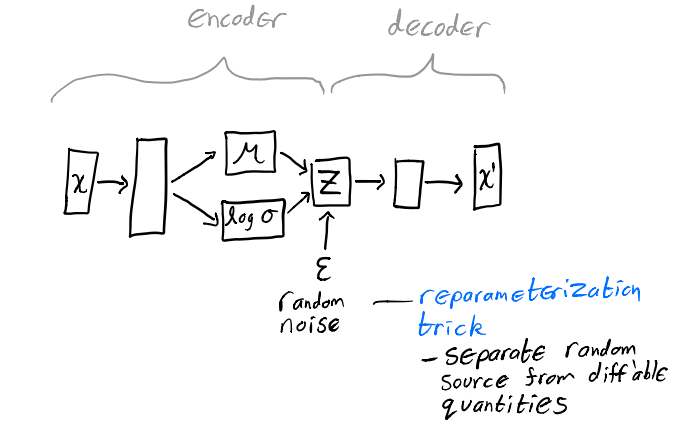
再来看一下 VAE 的实际架构。主要有两点值得细说。

第一点是，如果我们对每个 $X_i$ 找最最佳的 $q_\phi(Z|X_i)$，然后优化 $\phi$，这样的更新代价会很大。所以我们不这么做，而是去学习一个 inference 网络预测这个 $q_\phi(Z|X_i)$ 的均值和方差（实际上预测的是 $\mu$ 和 $log \space \sigma$），这样 inference 阶段的模型参数对于所有的数据参数是共享的，就可以分摊学习和更新的成本。

第二点是，采样的操作本身是不能反向传播的，所以采样这里用到了重参数化的技巧，也就是从 $\mathcal{N}(0,1)$ 中采样一个 $\varepsilon$，然后让 $Z=\mu + \varepsilon \times \sigma$，这样采样的操作就可以独立于网络之外，其他所有环节都能进行反向传播。

Stochastic Gradient Optimization of VLB

Todo…

参考

https://khoury.northeastern.edu/home/hand/teaching/cs7150-summer-2020/Variational_Autoencoders.pdf

https://www.youtube.com/watch?v=c27SHdQr4lw （力荐 👍）

最后修改于 2022-07-10